了解常用排序算法的时间复杂度,空间复杂度对于学好算法至关重要
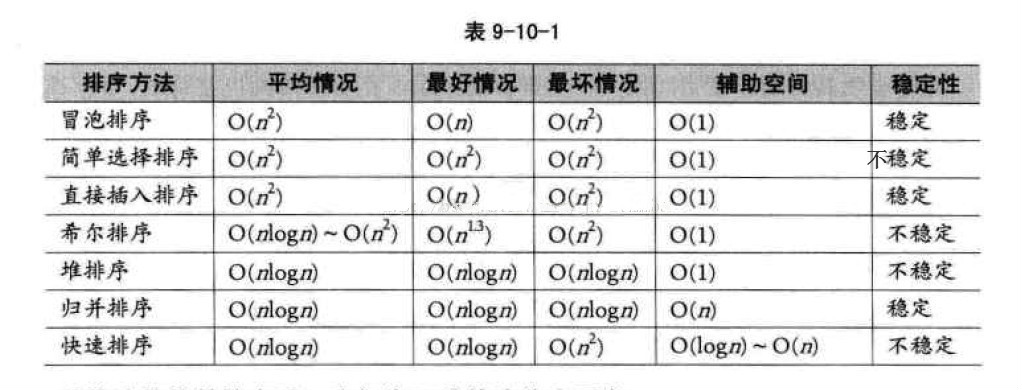
常用排序算法
1 归并排序
归并是所有排序算法中时间复杂度低的算法
时间复杂度: O(nlgn)
基本思想: 是一个分治策略,先进行划分,再进行合并
归并排序算法的核心: 先进行划分,再进行排序归并.归并两个有序的数组.即归并两个有序的数组A和B,然后就有了包含这两个新数组的数组C.
归并
function merge(left, right) {
var ret = [];
var Llen = left.length;
var Rlen = right.length;
var i = 0;
var j = 0;
while (Llen > 0 && Rlen > 0) {
if (left[i] > right[j]) {
ret.push(right[j++]);
Rlen--;
} else if (left[i] < right[j]) {
ret.push(left[i++]);
Llen--;
} else {
ret.push(left[i++]);
ret.push(right[j++]);
Llen--;
Rlen--;
}
}
while (Llen > 0) {
ret.push(left[i++]);
Llen--;
}
while (Rlen > 0) {
ret.push(right[j++]);
Rlen--;
}
return ret;
}
排序
// 排序
function mergeSort(arr) {
if(arr.length <= 1 ) {
return arr;
}
var mid = Math.floor(arr.length/2);
var left = arr.slice(0, mid);
var right = arr.slice(mid);
// 归并
return merge(mergeSort(left), mergeSort(right));
}
var arr = [9,8,7,6,5,4,3,2,1];
console.log(mergeSort(arr)); // [1,2,3,4,5,6,7,8,9];
2 二分查找
概念:二分查找又称折半查找
时间复杂度: O(lgn)
优点: 比较次数少,查找速度快,平均性能好
缺点: 要求待查表为有序表,且插入删除困难
适用于: 不经常变动而查找频繁的有序列表
过程: 首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
1.递归实现
function binarySearch(arr, start, end, num) {
var len = arr;
var binary = Math.floor((start + end) / 2);
if (num < arr[binary]) {
return binarySearch(arr, start, binary, num);
} else if (num > arr[binary]) {
return binarySearch(arr, binary, end, num);
} else {
return arr[binary];
}
}
var arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
var flag = binarySearch(arr, 0, 9, 2);
console.log(flag); // 2
2.非递归实现
// 非递归
function binarySearch(arr, dist){
var l = 0;
var h = arr.length - 1;
while(l <= h){
var mid = Math.floor((l+h)/2);
if(arr[mid] > dist){
h = mid - 1;
}else if(arr[mid] < dist){
l = mid + 1;
} else {
return arr[mid];
}
}
}
var arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
var number = binarySearch(arr, 1);
console.log(number); // 1